А.С. Белоусов, Е.И. Малиновский, С.В. Русаков, В.В. Самедов, П.Н. Шарейко

  ИССЛЕДОВАНИЕ ЭЛЕКТРОННО-ФОТОННЫХ
ЛИВНЕЙ В СВИНЦЕ ПРИ ЭНЕРГИИ 150-550 МЭВ
 
  Абстракт

         Измерены каскадные кривые и угловая расходимость ливней, образованных в свинце электронами с энергией в диапазоне от 150 до 550 МэВ.  Характеристики ливней определялись на основании анализа амплитудных распределений сцинтилляционного счетчика. Работа была выполнена на тормозных пучках электронных синхротронов С-25 и С-60. Полученные результаты представлены в работах [1,2].

         Схема эксперимента приведена на Рисунке 1. Фотоны тормозного пучка синхротрона, попадая на свинцовый конвертор толщиной 0.5 радиационной длины, рождают вторичные частицы (в подавляющем случае электронно-позитронные пары), часть из которых в соответствии с величиной импульса отбирается магнитным полем магнитного спектрометра М и направляется на установку. Моноэнергетические электроны, проходя через свинцовый коллиматор диаметром 30 мм, регистрировались мониторными счетчиками  S₁ и  S₂, которые выделяли пучок 15 х 15 мм ². Счетчик АS, имеющий отверстие диаметром 15 мм по оси пучка, был включен на антисовпадение с мониторными счетчиками.

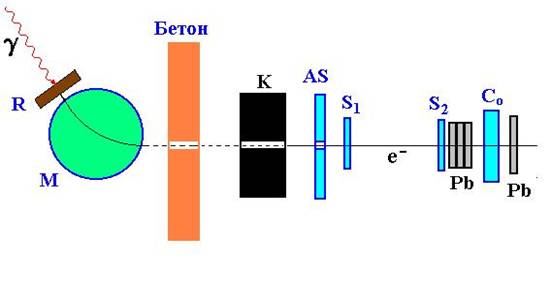
         Рисунок 1. Схема эксперимента по исследованию ливней в свинце:
М - магнитный спектрометр,  К - свинцовый коллиматор,   AS,  S₁ и S₂ - пучковые счетчики, С_о - спектрометрический сцинтилляционнй счетчик,  R - свинцовый конвертор, Pb - пластины свинцового радиатора.

         За счетчиком S₂  помещался свинцовый поглотитель переменной толщины - набор пластин толщиной в 1 радиационную единицу каждая. Для регистрации ливневых частиц применялся сцинтилляционный счетчик С_о, состоящий из из пластического сцинтиллятора размером 100х100х20 мм³ и фотоумножителя ФЭУ-78Б. Для нормировки данных в различных сериях измерений в счетчик был вмонтирован кристалл CsJ с  альфа источником  мощностью 100 распадов в секунду. Амплитудное разрешение по альфу-пику составляло ~ 2%. Использование пластического сцинтиллятора соответствовало введению порога обрезания спектра вторичных частиц, равного 5 МэВ - величина импульса от релятивистской частицы, прошедшей через пластик. Сигналы от счетчика поступали на амплитудный анализатор, который управлялся импульсами совпадений  S₁ и S ₂ при отсутствии сигнала в счетчике АS. Измерения были выполнены для электронов с энергией в диапазоне 150 - 550 МэВ с шагом 50 МэВ. Для каждой энергии толщина радиатора варьировалась от  t = 0  до   t = 9Х_о. При изменении расстояния между поглотителем и счетчиком С_о  регистрировались вторичные электроны с различными максимальными углами вылета относительно оси ливня. Помещение свинца за счетчиком давало возможность учитывать обратное рассеяние, т.е. регистрировать полное число заряженных частиц на данной глубине.

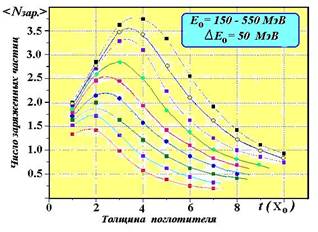
 Рисунок 2. Каскадные кривые Eo=5 МэВ,   для энергий первичных электронов от 150 до 550 МэВ.

         Распределение импульсов  А (Ео, Е, t, N) от счетчика С_о, где Е_о – начальная энергия электрона, Е – энергия обрезания регистрируемого спектра, t – толщина поглотителя, N – номер канала анализатора, при t = 0 имеет форму кривой распределения ионизационных потерь Ландау. При помещении перед счетчиком поглотителя в амплитудном спектре появляются пики, соответствующие одновременному прохождению через счетчик нескольких электронов. Среднее число частиц на выбранной глубине связанно с отношением Р(Е_о, Е, t) средних потерь на глубине t к средним потерям при t =0, которое определялось как отношение центров тяжести амплитудных распределений.

Р (Е_о, Е, t)  =  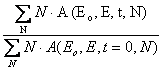=  sin d                          ( 1 )

Тогда среднее число частиц на глубине  t   n(Eo, E, t) будет равняться

                                                   n (Eo, E, t) = ,                                             (2)

где   - средний секанс угла отклонения вторичных электронов от оси ливня. Угловая расходимость частиц оценивалась из работ [3-4].  Полученные каскадные кривые представлены на Рисунке 2. На Рисунке 3. Приведены каскадные кривые электронов с энергией 200 МэВ при трех значениях максимальных углов вылета вторичных электронов. Из рисунка видно, что основная часть ливневых частиц вылетает под углами к оси ливня меньше 45⁰.

 

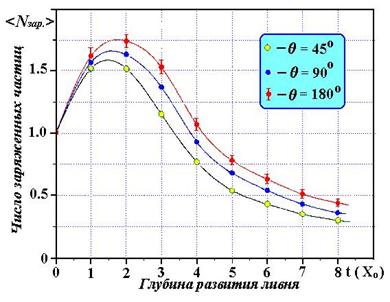
Рисунок 3. Каскадные кривые при различных максимальных углах
   регистрации вторичных электронов

    Важной характеристикой для описания каскадного процесса является интегральный пробег ливня при энергии обрезания Е:

I (E_o,E)  =  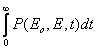 =                          3)

    Полученная по указанной формуле интегральная зависимость пробега от величины энергии первичного электрона представлена на Рисунке 4. Все экспериментальные точки в пределах ошибки ложатся на прямую линию. Интегральный пробег связан с энергией первичной частицы соотношением

                                     E_o =     I (E_o,E)   =   g(E_o,E)  I (E_o,E)                                    4)

   Среднее значение коэффициента      g(E_o, E )  при энергии обрезания   Е = 5 МэВ в диапазоне энергий до 550 МэВ составило 3.6 ±0.5 МэВсм²/г, или 23 МэВ/рад.ед.  Из соотношения (4), где ε_o – критическая энергия для свинца, равная 7.4 МэВ, находим коэффициент, учитывающий величину энергии обрезания:

                                                        P(E_o, E =5 МэВ) = 0.32 ± 0.04.

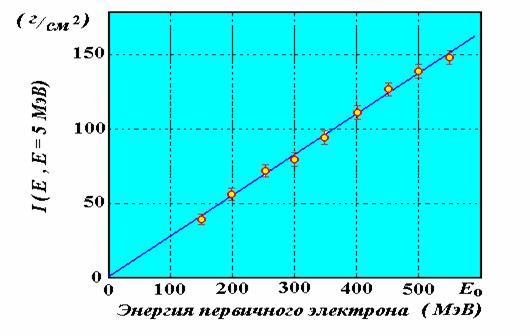
             Рисунок 4.   Зависимость величины интегрального пробега ливня от  энергии первичного электрона.

      Таким образом более двух третей энергии линя рассеивается электронами с энергией меньшей 5 МэВ.Для сравнения на Рисунке 5 приведены экспериментально измеренные каскадные кривые для энергии первичного электрона Е_о = 200 МэВ  при энергии обрезания Е = 1 МэВ [4] и Е = 5 МэВ (данная работа) вместе с результатами расчета для  Е = 1.5 и 2.5 МэВ [5] и   E  = 10 МэВ [3].

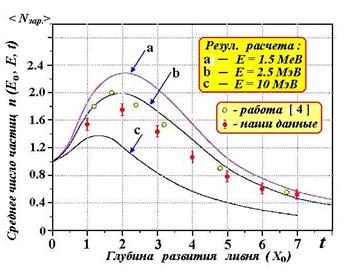
                            Рисунок 5. Сравнение экспериментальных данных   c  результатами расчета.
 
 

Литература.

 1. А.С. Белоусов, Е.И. Малиновский, С.В. Русаков, В.В. Самедов, П.Н. Шарейко

     Ядерная физика. Т.17, вып. 5, стр. 1028-1033, (1973)

2. А.С. Белоусов, Н.П. Буданов, Я.А. Ваздик, Б.Б. Говорков, Е.И. Малиновский

    Труды ФИАН, том 143,  стр. 100-111, Москва, Изд. «Наука» (1983)

3. D. Crawford, H, Messel    Rhys. Rev. v. 128, p.235 (1962)

4. О.А. Займидорога, Ю.Д. Прокошкин, М.В. Цупко-Ситников

    ЖЭТФ, том 51. стр. 749 (1966)

5. H. Nagel, C. Achlier   Zs. Phys. V. 175, p. 464  (1963)