А.С. Белоусов,  Н.П. Буданов,  Я.А. Ваздик,  Б.Б. Говорков,  Е.И. Малиновский,  С.В. Русаков, В.И. Сергиенко,  Е.И. Тамм, П.Н. Шарейко
 
 

           СЕЧЕНИЕ   РОЖДЕНИЯ   ПАР   ФОТОНАМИ НА ВОДОРОДЕ

     Работа выполнена в период   1971 - 1972 г.г. на электроном пучке [1] протонного синхротрона  У-70  в  Протвино  с использованием установки “Гамма-е” . Схема установки приведена на Рисунке 1. Описание отдельных узлов установки приведено в работах [2,3],   полученные результаты представлено в  [3,5].
 

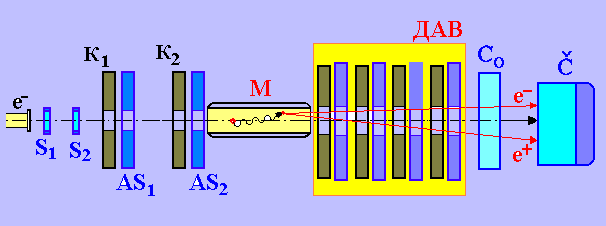
                Рисунок 1.  Блок-схема эксперимента по исследования  рождения  е⁺е^- - пар на водороде: 
К1  и  К2 -   колиматоры, S₁ , S₂ , АS₁ , АS_{2 , -} сцинтилляционные счетчики, С ₀ - счетчик ионизационных потерь,                 С - черенковский ливневой спектрометр,  М - мишень,   ДАВ - детектор адронных взаимодействий
 

Аннотация

             Прохождении моноэнергетического электронного пучка через спектрометрический сцинтилляционный счетчик с тонким сцинтиллятором (счетчик ионизационных потерь dE/dX) характеризуется спектром импульсов с распределением
Р ₁ (N),  соответствующим  распределению   Ландау,   где  N  -  номер канала  амплитудного  анализатора   ( величина энерговыделения в счетчике), а Р(N) - нормированное число импульсов в канале (число частиц с данной энергией). Если через счетчик в каждом событии постоянно проходит две частицы , то спектр амплитуд в счетчике потерь будет описываться распределением P ₂ (N) , где

                                                  P ₂ ( N ) = Σ P ₁( K ) · P ₁ (N - K) (1)                                                                 (1)

      Отношение центров тяжести распределения P ₂ (N) и P ₁ (N) будет равно двум. В случае переменного числа частиц n , проходящих через счетчик  в каждом событии, отношение площади под  распределением   P _n ( N )  к  площади  под распределением Ландау  для потерь одиночной  частицы  даст  среднее  число частиц   < n >   по всем событиям. Это обстоятельство и было использовано в описанных ниже измерениях.
 

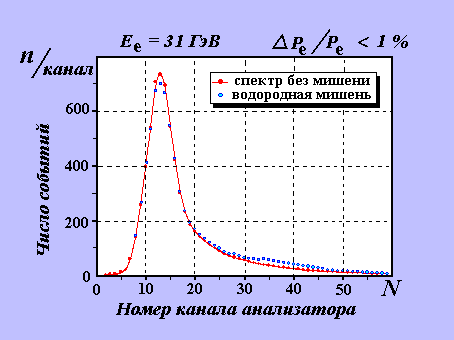
             Рисунок 2. Спектры ионизационных потерь электронов в счетчике С _О с мишенью и без мишени М   (нормировка по числу электронов, прошедших через установку).

        Измерения проводились на электронном пучке Серпуховского ускорителя при следующих характеристиках пучка: энергия Е _е = 31 ГэВ,  разброс по импульсу частиц в пучке  ΔР / Р < 1%, интенсивность не выше 10³ частиц в секунду. Схема эксперимента показана на Рисунке 1. Электронный пучок формировался магнитооптической системой канала и системой из двух свинцовых коллиматоров  К ₁  и  К ₂   и двух охранных счетчиков  AS ₁ и  AS₂, имеющих отверстия в центре диаметром 40 мм для прохождения пучка. Мониторирование пучковых частиц проводилось сциллянционными счетчиками S ₁ и S ₂, включенными на совпадение, и черенковским ливневым спектрометром С [3], который имел порог регистрации на уровне ~ 15 ГэВ. Жидководородная мишень М служила одновременно радиатором, в котором электроны пучка испускали фотоны вследствие радиационного торможения, и мишенью, с которой взаимодействовали γ-кванты.
После мишени располагалась система регистрации продуктов адронных взаимодействий, представляющая из себя 4 сцинтилляционных счетчика 50 х 50 см, прослоенных пластинами свинца  ( ДАВ ). Спектр импульсов от сцинтилляционного счетчика ионизационных потерь, обозначенного на схеме С_о , поступал на амплитудный анализатор, который управлялся совпадением сигналов от S ₁, S ₂ и С, при отсутствии запрещающих сигналов от АS _1, АS ₂ и  ДАВ.

На Рисунке 2 показаны амплитудные распределения (повторяющие форму распределения Ландау) от счетчика С_о при наличии в пучке водородной мишени - Р _Н (N) и без нее - Р _О (N). Для определения сечений образования пар проводился анализ разности распределения потерь с мишенью и без нее. Как видно из    Рисунка 3,   где показана разность
 

       Рисунок 3. Разность нормированных спектров ионизационных потерь электронов в счетчике С _О с мишенью и без мишени М.

            К ( N )  =  Р _Н ( N ) - Р _О ( N ).                                                          (3)
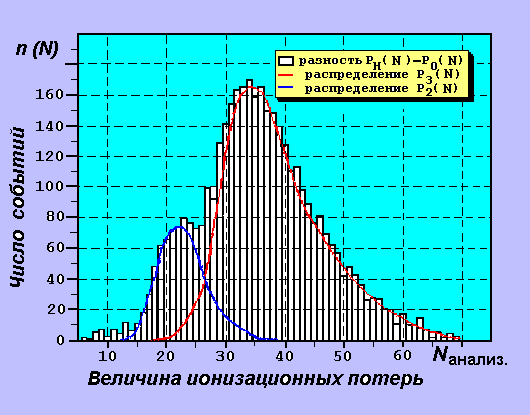
       Интересующее  нас распределение имеет два четко выраженных максимума.     Низкоэнергетический  максимум соответствует прохождению двух,   связанных во времени электронов,  и  может быть ответственным  за  Меллеровское рассеяние. Наличие трех частиц в конечном состоянии приводит к появлению второго максимума.  Вклад  в него дают  такие процессы,  как испускание электроном  γ-кванта с  дальнейшим  образованием электрон-позитронных пар,  а также непосредственное рождение пар электронами. Выделение  из экспериментального распределения  событий, которые ответственны за наличие трех частиц в счетчике С_о, проводилось путем вычитания из суммарного распределения кривой (1) , пронормированной в точке N = 2 N _М, где N _М соответствует наиболее вероятным потерям при прохождении одной частицы - абсцисса максимума кривой Р _О ( N ). Следует отметить, что если е ⁺ е ^-  пара рождалась фотоном малой энергии, то одна из компонент пары может выйти из области пучка и не попасть в С_О. А так как эффективность детектора адронных взаимодействий  к  электронам в этой области  низка [4],  и  частица  не может эффективно регистрируется в ДАВ, то это событие воспринимается как процесс с двумя частицами, т.е. существует некий порог по энергии для регистрации процесса рождения пар.  Моделирование для данной геометрии установки дало для порога величину порядка Е _пор = 200-240 МэВ.
       Число событий с тремя частицами в С_О можно представить как:

                 n ₃ = N_O ·n _H · L σ (e → 3e)  +  N_O · n _H  σ (γ → 2e)                    (3)

    где N_O - число электронов, прошедших через мишень,    n _H - число ядер водорода в 1 см ^3,    L - длина мишени,        σ (γ → 2e) - сечение образования пар фотонами, σ(e → 3e) - сечение непосредственного образования пар электронами с энергией 31 ГэВ. Разбив  в (3)  область интегрирования на два энергетических интервала: от 200 МэВ до 10 ГэВ и от 10 ГэВ до 31 ГэВ, вычислили значение интеграла в первой области, используя имеющиеся в литературе данные об сечениях фоторождения пар на водороде [5]. Учитывая тот факт, что при изменении первичных частиц от 10 до 30 ГэВ отношение R, определяемое как

                                 R = σ (e → 3e) / σ (γ →2e)                                                          (4)

изменяется от 0.127 до 0.156 [6], и cчитая, что сечение фоторождения пар мало меняется в указанной области, мы, приравняв   σ(e → 3e) при энергии 31 ГэВ    величине 0.153 = σ(γ →е⁺ е^-) (среднее значение сечения фоторождения пар в области 10 - 30 ГэВ), можем вычислить [7,8]:

                                           σ (γ → е⁺ е ^-) = (21.62 ± 0.48) · 10^-27 см²
 

Литература.
 

  1.    С.С. Герштеин, А.В. Самойлов, Ю.М. Сапунов и др.
        Атомная Энергия, т. 35, вып.3, стр. 181-184, Москва, 1973
  2.   А.С. Белоусов, Н.П. Буданов, Я.А. Ваздик и др.
       Препринт ФИАН, №125, Москва, 1974
  3.   А.С. Белоусов, Я.А. Ваздик, Е.И. Малиновский и др.
       ПТЭ, № 6, стр. 33-35, Москва, 1973
  4. А.С. Белоусов, Я.А.Ваздик, Е.И. Малиновский и др.
       Препринт ФИАН № 66, Москва, 1973
  5. А.С. Белоусов, Н.П. Буданов, Я.А. Ваздик и др.
      Труды ФИАН СССР, т.143 (1983) стр. 100-104